カテゴリー: 過去問演習

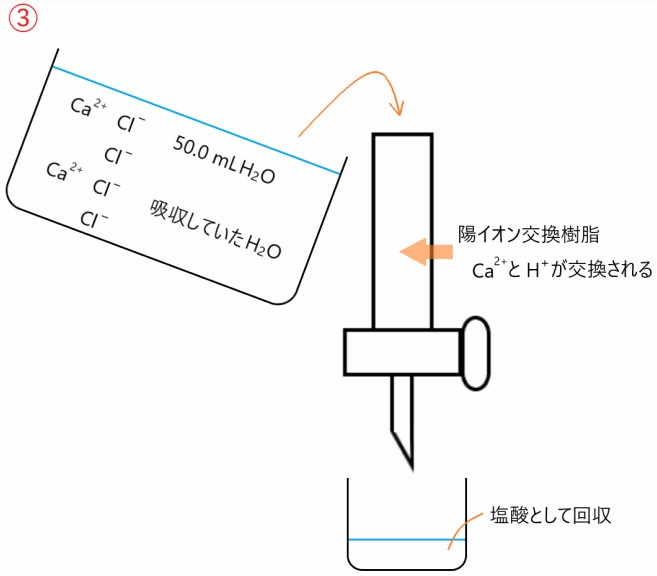
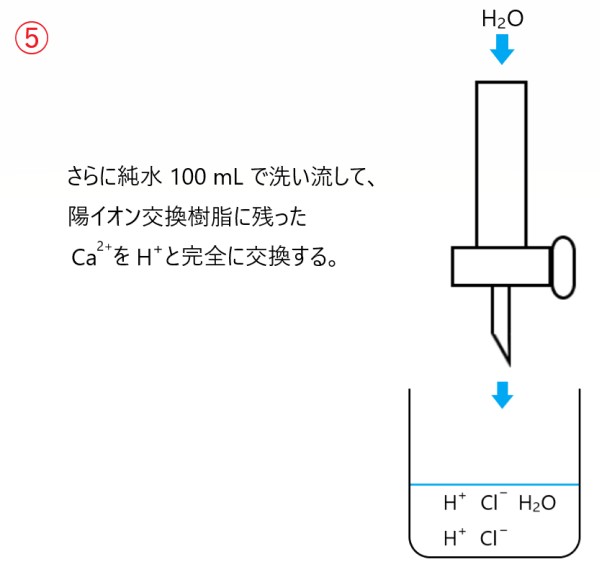
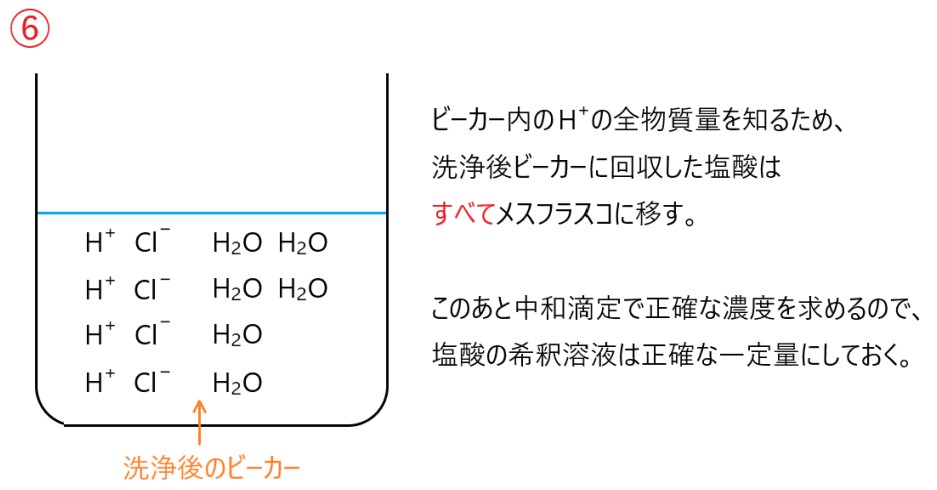
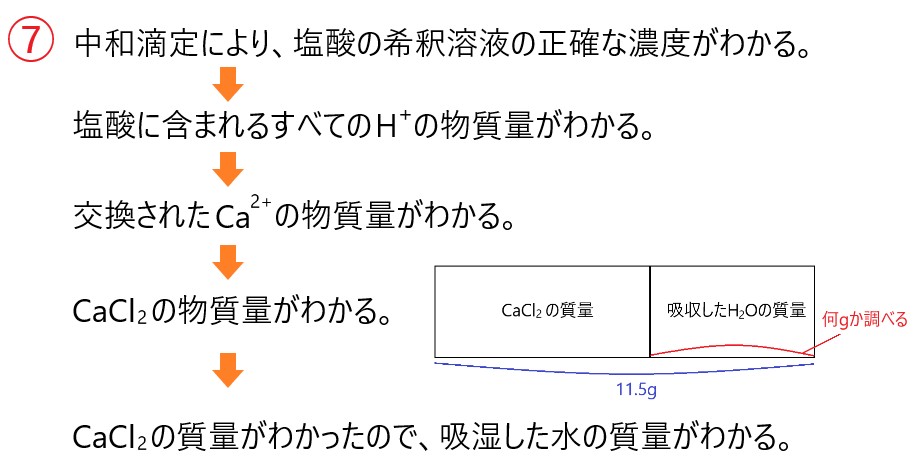
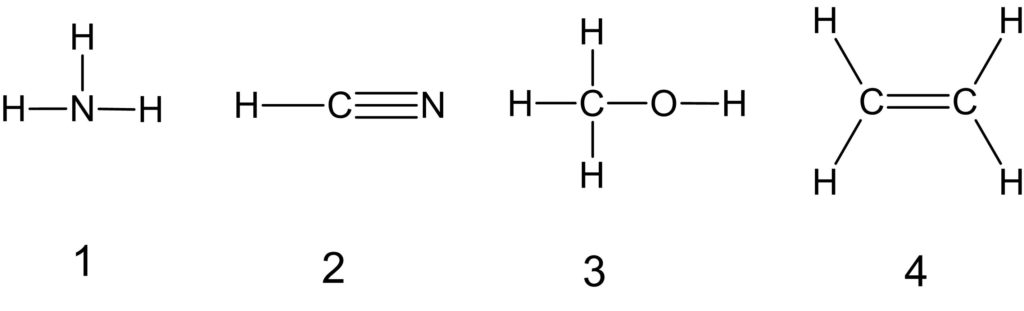
第1問

問1　正解　a　1　　　b　4

アは電子の数が 2 なので、原子番号 2 の He の電子配置と同じです。

同様にイは原子番号 6 の C の電子配置、ウは原子番号 10 の Ne の電子配置、エは原子番号 11 の Na の電子配置、オは原子番号 17 の Cl の電子配置と同じです。

a

1 価の陽イオンとして（ 1 個の電子を放出して）アの電子配置となるのは、原子番号 3 の Li です。

また 1 価の陰イオンとして（ 1 個の電子を受け取って）ウの電子配置となるのは、原子番号 9 の F です。

これらが化合物となるので、①が正解です。

b

1　〇　He は K 殻が電子 2 個で満たされて閉殻となっており、化学的に反応性の乏しい希ガス（貴ガス）です。そのため他の原子とは結合しにくいです。

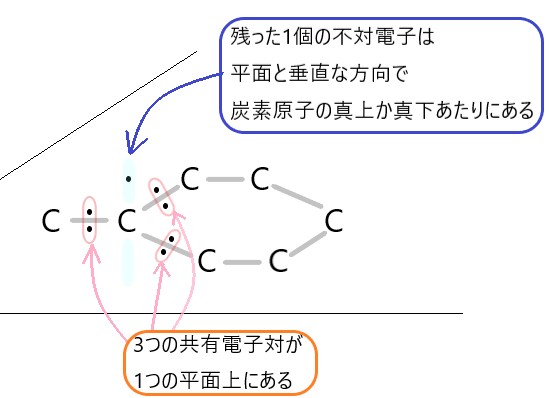
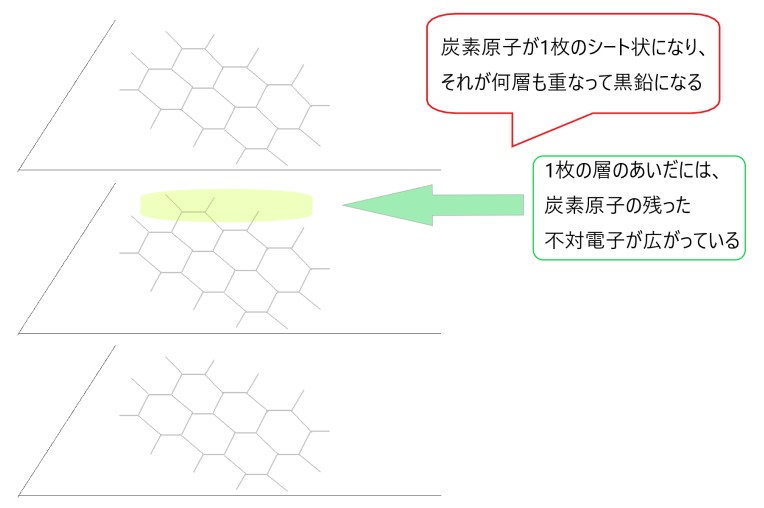
2　〇　C は 4 つの不対電子をもち、単結合、二重結合、三重結合をつくることができます。

3　〇　He 、Ne 、Ar などの希ガス（貴ガス）は、常温・常圧で気体です。

4　×　電子を放出して陽イオンとなるのに必要なエネルギーが、イオン化エネルギーです。周期表の左下の元素（最外殻の電子数が少ない元素）は、イオン化エネルギーが小さくなる傾向です。

5　〇　Cl は不対電子を 1 個もつので、H と共有結合をつくり HCl 分子となります。

問2　正解　1

1　〇　①の記述は蒸留（分留）の説明です。石油は蒸留（分留）によって成分を分離します。石油は加熱すると、沸点の異なる成分が順番に気体となって分離できます。

2　×　②の記述は昇華法の説明です。

3　×　③の記述は抽出の説明です。

4　×　④の記述は再結晶の説明です。

問3　正解　6

ア　塩化ナトリウム NaCl は、Na⁺ と Cl^－ がクーロン力でイオン結合したイオン結晶です。

イ　ケイ素 Si は、共有結合の結晶をつくります。

ウ　カリウム K は金属なので、金属結晶です。

エ　ヨウ素 I₂ は、分子が分子間力によって配列されてできた分子結晶です。ただし I₂ は分子なので、ヨウ素 I 原子同士は共有結合でつながっています。

オ　酢酸ナトリウム CH₃COONa は、CH₃COO^－ と Na⁺ からできたイオン結晶です。ただし酢酸イオン CH₃COO^－ は、共有結合でイオンが構成されています。

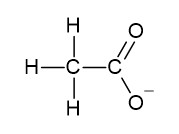
以上より、イ・エ・オが当てはまります。

問4　正解　5

1　〇　100 K のグラフの曲線を見ると、横軸 240 m/s にピークの山があります。したがって、速さが 240 m/s である分子の数の割合が最も高いといえます。

2　〇　横軸が 240 m/s の位置で垂直に上にグラフを見ていくと、はじめに 500 K の曲線があり、次に 300 K 、最後に 100 K の曲線があります。

したがって、分子の数の割合が最も少ないのが 500 K で、次に少ないのが 300 K 、分子の数の割合が最も多いのが 100 K とわかります。

3　〇　横軸が 800 m/s の位置で垂直に上にグラフを見ていくと、はじめに 100 K の曲線があり、次に 300 K 、最後に 500 K の曲線があります。

したがって、分子の数の割合が最も少ないのが 100 K で、次に少ないのが 300 K 、分子の数の割合が最も多いのが 500 K とわかります。

4　〇　3 つの曲線を見ると、100 K 、300 K 、500 K と温度が上がるにつれて、分子の数の割合の曲線はピークの高さが低くなり、横への広がりが大きくなります。

低い温度ではゆっくりとした速さの分子が多いですが、温度が上がると分子の速さの値が大きい分子が増え、分子の速さの分布は右側へ広がっていきます。

5　×　500 K では、540 m/s の速さをもつ分子の数の割合が最も多いです。（ 500 K では分子の速さの分布のピークが 540 m/s です。）

1000 K になると、分子はさらに速く動くようになるので、分布は 500 K より右側にずれて広がります。

分布のピークが 540 m/s より右に移動し、分布のグラフの山も平らに広がるので、540 m/s の速さをもつ分子の数の割合は減少すると考えられます。

問5　正解　1

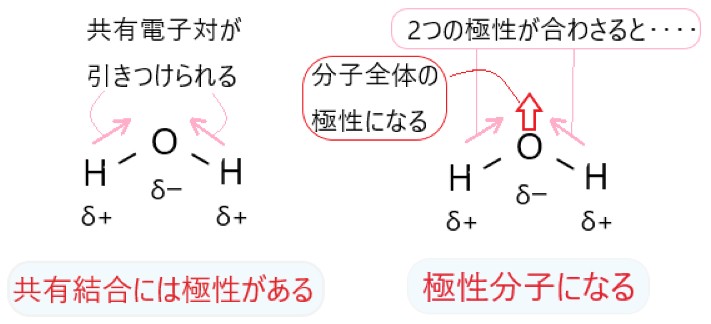
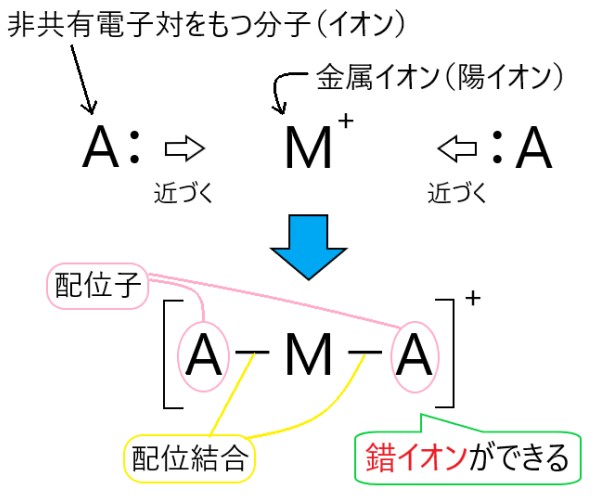
1　〇　アンモニア NH₃ の窒素原子は 1 つの非共有電子対をもつので、これを電子を失っている H⁺ に提供して、アンモニウムイオン NH₄⁺ となります。

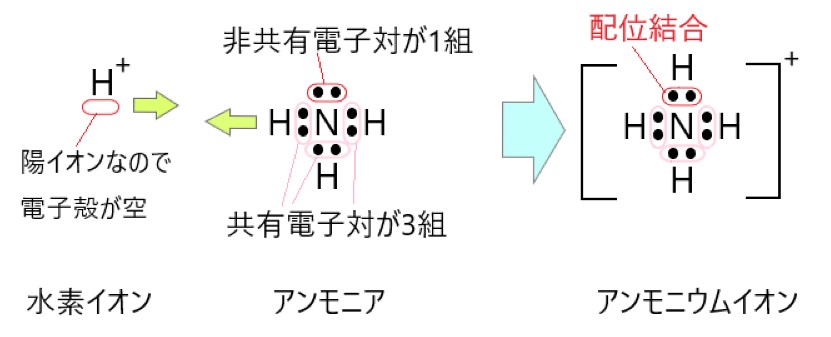
2　〇　配位結合は、一度それができてしまうと、他の共有結合と同等になります。

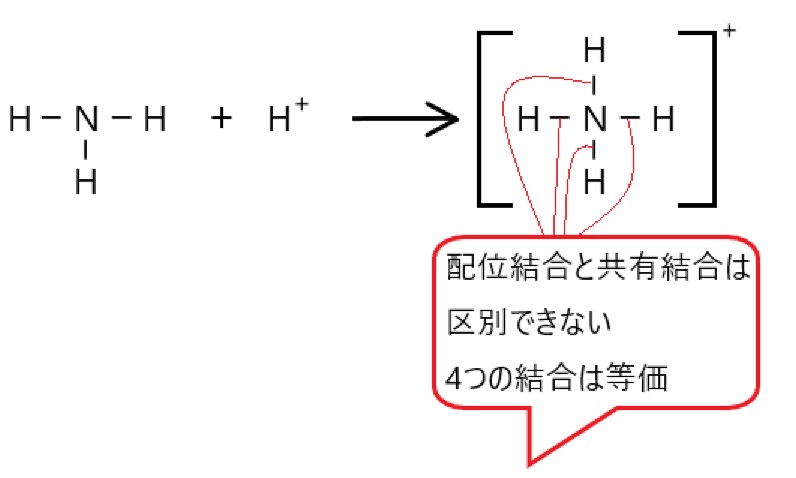
3　〇　配位結合は、非共有電子対をもつ原子が 、2 つの電子を他の原子やイオンに提供することでできます。

以下は非共有電子対をもつ原子を含む分子が、金属イオンと配位結合する模式図です。

問6　正解　2

濃度不明の希硫酸 H₂SO₄ 10.0 mL と、0.10 mol/L の塩酸 HCl 20.0 mL から得られる H⁺ の物質量を式で表します。

これが 0.50 mol/L の 水酸化ナトリウム NaOH 水溶液 20.0 mL から得られる OH^－ の物質量と等しくなります。

H₂SO₄ は 2 価の酸、HCl は 1 価の酸、NaOH は 1 価の塩基なので、濃度不明の希硫酸の濃度を C mol/L とすると、

$$C mol/L　×　2　×　\frac{10.0 mL}{1000 mL}　+　0.10 mol/L　×　1　×　\frac{20.0 mL}{1000 mL}$$

$$=　0.50 mol/L　×　1　×　\frac{20.0 mL}{1000 mL}$$

これを解くと、C = 0.40 mol/L

問7　正解　6

Fe₂O₃ では、酸素原子 O の酸化数は －2 、化合物全体の酸化数の和は 0 なので、

鉄原子 Fe の酸化数は　Fe × 2 + (－2) × 3 = 0　より +3 となります。

鉄 Fe の単体では Fe の酸化数は 0 、酸素 O₂ の単体でも O の酸化数は 0 です。

したがって Fe の酸化数は 0 → +3 、O の酸化数は 0 → －2 と変化します。

問8　正解　ア　4　　　イ　3

鉛 Pb は、二次電池である鉛蓄電池の電極として用いられます。また Pb の板は放射線を通さないので、放射線が発生する現場（病院の放射線診療室など）で遮蔽板として使われます。

銀 Ag は、金属の中で最もよく熱や電気を伝えます。二番目に熱伝導性や電気伝導性が高い金属は銅 Cu です。

問9　正解　4

除去された SiO₂ の質量は　2.00 g － 0.80 g = 1.20 g　です。

Si の原子量は 28 、O の原子量は 16 なので、SiO₂ の式量は　28 + 16 × 2 = 60　です。

1.20 g の SiO₂ の中に含まれるケイ素原子 Si の質量は

1.20[g] × \(\frac{28}{60}\) = 0.56[g]

したがって求めるケイ素 Si の含有率は

\(\frac{0.56[g]}{2.00[g]}\) × 100 = 28 %

です。

第2問

問1　正解　a　ア　2　　イ　3　　ウ　5　　　b　1

a

カリウム K の原子番号は 19 で、カリウム原子のもつ陽子の数と電子の数は 19 です。電子配置は K 殻に 2 個、L 殻に 8 個、M 殻に 8 個、N 殻に 1 個となります。

カリウムイオン K⁺ は 1 個の電子が失われるので、原子核の陽子は 19 個、電子は K 殻に 2 、L 殻に 8 、M 殻に 8 の配置となります。

同様にカルシウム Ca の原子番号は 20 で、カルシウム原子のもつ陽子の数と電子の数は 20 です。電子配置は K 殻に 2 個、L 殻に 8 個、M 殻に 8 個、N 殻に 2 個となります。

カルシウムイオン Ca²⁺ は 2 個の電子が失われるので、原子核の陽子は 20 個、電子は K 殻に 2 、L 殻に 8 、M 殻に 8 の配置となります。

以上のように、Ca²⁺ では原子核中に存在する粒子である陽子の数が K⁺ より多く、原子核の正電荷が大きいです。

そのため Ca²⁺ の方が、静電気的な引力で強く電子殻の電子を引きつけるので、イオン半径は小さくなります。

b

KNO₃ の溶解度曲線を見ると、 40 ℃で 64 g となっています。つまり 40 ℃では KNO₃ は水 100 g に 64 g まで溶けます。

今 40 ℃の KNO₃ の飽和水溶液 164 g があるので、これは水 100 g に KNO₃ を 64 g 溶かしたということです。

一方、25 ℃では KNO₃ の溶解度は 38 g です。これは水 100 g に KNO₃ が最大 38 g 溶けることを示します。

40 ℃で水 100 g に溶解している 64 g の KNO₃ は、25 ℃で 38 g までしか溶解しないので

64 － 38 = 26 g の KNO₃ が析出します。

KNO₃ の式量は 101 なので、析出する KNO₃ の物質量は

\(\frac{26[g]}{101[g/mol]}\) ≒ 0.26 mol

問2　正解　a　3　　　b　4　　　c　2

a

まず BaCl₂ 水溶液の滴下量の値を横軸、電流の大きさを縦軸として方眼紙にプロットして（点をつけて）みましょう。

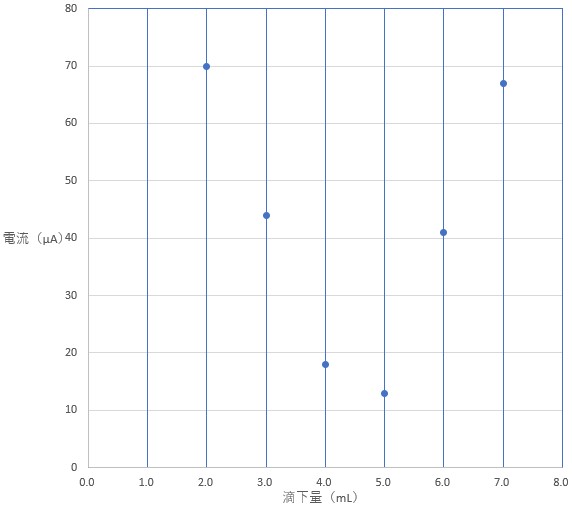
6 つの測定点をどのように見たらよいでしょうか。

2.0 、3.0 、4.0 mL と滴下量が増えると電流の値が小さくなり、さらに 5.0 、6.0 、7.0 mL と滴下量が増えると電流の値が大きくなるように見えます。

これは問題文の説明から考えて、2.0 ～ 4.0 mL では BaCl₂ を滴下すると沈殿を生じる反応が進み、水溶液中の Ag⁺ イオンと SO₄^2－ イオンが減少したために電流が流れにくくなったと推測できます。

反応が進み沈殿が生成するあいだは、滴下した BaCl₂ はすべて沈殿するので、Ba²⁺ イオンや Cl^－ イオンは水溶液中で増えません。

滴下量が 5.0 ～ 7.0 mL のときは、BaCl₂ の滴下により水溶液中の Ag⁺ イオンと SO₄^2－ イオンは沈殿反応で消費され、既に存在しません。

5.0 ～ 7.0 mL では、BaCl₂ の滴下によって増えた Ba²⁺ 、Cl^－ イオンが電気を通します。

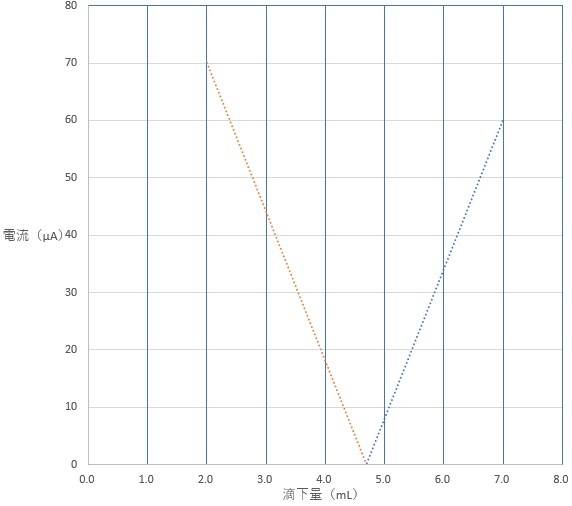
完全に沈殿反応が終了したときを調べるため、滴下量 2.0 、3.0 、4.0 mL の点を通るような直線を近似として、 滴下量 5.0 、6.0 、7.0 mL の点を通るような直線を近似として、2 直線を方眼紙にひきます。

理想では、この 2 直線は電流の値が 0（縦軸の値が 0 ）の点で交わります。

この電流の値 0 の点が、水溶液中にイオンが存在しないときであり、すなわち Ag₂SO₄ が完全に反応したときです。（以下は理想的なグラフです。）

実際に方眼紙に書き込むと次のようなグラフになります。（実験のデータなので、理想的な形状にはなりません。）

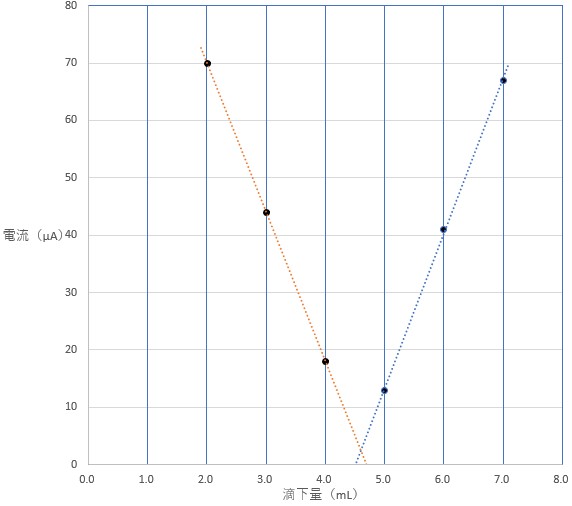
グラフより、滴下量 4.6 mL が正解です。

b

Ag₂SO₄　+　BaCl₂　　→　　BaSO₄ ↓　+　2 AgCl ↓

と反応するので、Ag₂SO₄ 1 mol から AgCl の沈殿は 2 mol 生成します。

0.010 mol/L のAg₂SO₄ 水溶液 100 mL が完全に沈殿したとき、Ag₂SO₄ の物質量は

0.010[mol/L]　×　\(\frac{100[mL]}{1000[mL]}\)[L]　=　0.0010[mol]

ありました。

AgCl の式量は 143.5 なので、生成する沈殿 AgCl の質量は

0.0010[mol]　×　2　×　143.5[g/mol]　≒　0.29[g]

c

Ag₂SO₄ と BaCl₂ は 1：1 の物質量の比で反応します。

BaCl₂ 水溶液を 4.6 mL 滴下すると完全に反応するので、b で計算した Ag₂SO₄ の物質量 0.0010 mol の値を使います。

BaCl₂ 水溶液のモル濃度を C mol/L とすると、

0.0010[mol]　=　C[mol/L]　×　\(\frac{4.6 mL}{1000 mL}\)[L]

これを解くと

C　=　\(\frac{1}{4.6}\)　≒　0.22[mol/L]

第1問

問1　正解　6

空気は窒素 N₂ や酸素 O₂ 、アルゴン Ar 、二酸化炭素 CO₂ など多くの純物質が混ざっているので、混合物です。その存在比は窒素 N₂ が約 78 %、酸素 O₂ が約 21 %、アルゴンが約 0.93 %、二酸化炭素が約 0.04 % ‥‥となっています。

メタンは CH₄ という化学式で表される純物質です。CH₄ は C と H の二つの元素からできている物質なので、化合物です。

オゾンは O₃ という化学式で表される純物質です。 O₃ は酸素元素 O のみからできており、一つの元素でつくられている物質なので単体です。

以上より、正解は⑥です。

問2　正解　2

1　0 ℃、1.013 × 10⁵ Pa の状態で体積が 22.4 L の気体の物質量は 1 mol です。

したがってこの酸素 O₂ の物質量は 1 mol です。

気体の酸素 O₂ では、1 個の O₂ 分子のなかに酸素原子は 2 個あります。

そのため、1 mol の O₂ には 2 mol の酸素原子が含まれます。

2　水 H₂O の分子量は、　1.0 × 2 + 16 = 18　です。

分子量が 18 なので、モル質量は 18 g/mol となります。

したがって 18 g の水 H₂O の物質量は\(\frac{18[g]}{18[g/mol]}\) = 1.0 mol

水 H₂O の 1 分子のなかに含まれる酸素原子は 1 個なので、水 18 g に含まれる酸素原子の物質量は 1.0 mol です。

3　過酸化水素 H₂O₂ の分子が 1 個あるとき、それに含まれる酸素原子は 2 個です。

したがって H₂O₂ が 1.0 mol あれば、それに含まれる酸素原子の物質量は 2.0 mol です。

4　黒鉛 C を完全燃焼させたときの化学反応式は

C　+　O₂　→　CO₂

したがって黒鉛 C が 1 mol 反応すれば、CO₂ は 1 mol 生成します。

ここで C の原子量は 12 なので、

黒鉛 12 g の物質量は\(\frac{12[g]}{12[g/mol]}\) = 1.0 mol

よって CO₂ は 1.0 mol 生成しています。

1 個の CO₂ 分子には 2 個の酸素原子が含まれるので、1.0 mol の CO₂ に含まれる酸素原子の物質量は 2.0 mol です。

以上より、①、③、④の酸素原子の物質量は 2 mol であり、②の酸素原子の物質量は 1 mol です。

問3　正解　a　3　　　b　40　10

原子番号が増えていくと、つまり陽子の数（電子の数）がひとつずつ増えていくと、それぞれの原子はどうなるのかという問題です。

a

原子番号は陽子の数と一致しますので、これに当てはまるのはイのグラフです。

価電子の数は、原子の最外殻の電子数と一致します。ただし希ガス（貴ガス）の元素は価電子の数が 0 です。

具体的に考えると、原子番号 1 の H では、最外殻電子数が 1 なので価電子の数は 1 です。原子番号 2 の He は、希ガス（貴ガス）の元素なので価電子の数は 0 です。原子番号 3 の Li は、最外殻電子数が 1 なので価電子の数は 1 です。

これを続けていくと、ウが価電子の数のグラフであるとわかります。

残りのアが、中性子の数のグラフとなります。

中性子の数はだいたいその原子の陽子の数と同じ程度ですが、原子によって少しばらつきます。

b

質量数　=　陽子の数　+　中性子の数

となるので、アのグラフの値とイのグラフの値の和が最大となる原子を求めます。

これをグラフから読み取ると、原子番号 18 の Ar が陽子の数 18 、中性子の数 22 となり、和（質量数）が最大です。

したがって最大の質量数は　18 + 22 = 40　となります。

次に M 殻に電子がなく、原子番号が最大の原子を考えます。

原子の電子配置では、はじめに 2 個の電子が K 殻に入り、次に 8 個の電子が L 殻に入ります。その次に電子は M 殻に入っていきます。

そのため、M 殻に電子が入るまでに K 殻と L 殻で 10 個の電子が入ります。10 個の電子が入る原子が、原子番号が最も大きくなるので、求めるこの原子の原子番号は 10 です。

問4　正解　5

金属結晶は自由に結晶内を動ける自由電子をもつので、電気を通します。

分子結晶は分子が規則正しく並んだ固体なので、動ける電子やイオンがなく、電気を通しません。

また、多くの共有結合の結晶も自由に動ける電子やイオンをもたないので、電気を通しません。

ただし例外として、共有結合の結晶である黒鉛は電気を通します。これは黒鉛の構造によるものです。

黒鉛は炭素原子がまわりの 3 つの炭素原子と 120° の角度で共有結合し、正六角形の構造をつくっています。

このとき、炭素原子は 4 つの不対電子のうち 3 つを共有結合に使っていますが、残りの 1 つの電子は黒鉛の平面構造の層のあいだにあります。

正六角形の繰り返し構造により炭素原子が平面に並び、これが何層も重なって黒鉛ができています。この層のあいだにある電子が動くので、黒鉛は電気を通します。

問5　正解　4

イオン化傾向の大きな金属は反応性が高く、イオン化傾向の小さな金属は化学的に安定です。

Li 、K 、Ca 、Na は常温の水と反応します。

Mg は熱水と反応します。

Al 、Zn 、Fe は高温の水蒸気と反応します。

Ni よりイオン化傾向の小さい金属は、水と反応しません。

問6　正解　4

1　×　CO は Fe₂O₃ から酸素を受け取り CO₂ となるので、酸化されています。自身が酸化されているので、CO は還元剤です。

CO のうちの炭素原子 C の酸化数は +2 → +4 と変化しています。（酸素原子 O は －2 のまま）

2　×　NH₄Cl は弱塩基 NH₃ と強酸 HCl から生成した弱塩基の塩です。これが強塩基 NaOH と反応し、弱塩基の NH₃ が遊離しています。

これは酸塩基の反応であり、酸化数に変化はありません。

3　×　Na₂CO₃ は弱酸 H₂CO₃ と強塩基 NaOH から生成した弱酸の塩です。これが強酸 HCl と反応し、弱酸の塩の NaHCO₃ と強酸の塩の NaCl が生成しています。

さらに HCl を加えた場合は

Na₂CO₃　+　2 HCl　　→　　2 NaCl　+　H₂O　+　CO₂

となり、弱酸の H₂CO₃ が遊離します。

（H₂CO₃ はすぐに分解して、H₂O と CO₂ になります。）

この反応は酸塩基の反応なので、酸化数に変化はありません。

4　〇　これは Br₂ が酸化剤、KI が還元剤である酸化還元反応です。

Br₂ のうちの臭素原子 Br の酸化数は 0 → －1 と変化し、還元されています。

KI のうちのヨウ素原子 I の酸化数は －1 → 0 と変化し、酸化されています。

（カリウム原子 K の酸化数は +1 のまま）

問7　正解　1

100 mL の溶液の質量は、密度との積として求められます。（100 mL = 100 cm³ ）

100[cm³]　×　d[g/cm^3]　=　100d[g]

この溶液に含まれる溶質の質量は、質量パーセント濃度が x %なので、

$$100d[g] \times \frac{x}{100} = xd[g]$$

となります。

溶質のモル質量が M[g/mol] なので、質量が xd[g] である溶質の物質量は

$$\frac{xd}{M}[mol]$$

問8　正解　5

問題文で示されたイオン反応式から、

正極では 4 mol の電子が流れると 2 mol の水が生成し、負極では 2 mol の電子が流れると 1 mol の水素が消費されるとわかります。

すなわち正極では 2 mol の電子が流れると 1 mol の水が生成します。

まとめると、2.0 mol の電子 e^－ が流れると 1.0 mol の水 H₂O が生成し、1.0 mol の水素 H₂ が消費されます。

1.0 mol の水 H₂O の質量は、H₂O の分子量が 18 なので 18 g です。

1.0 mol の水素 H₂ の質量は、H₂ の分子量が 2.0 なので 2.0 g です。

以上より、⑤が正解です。

第2問

問1　正解　a　3　　　　b　3

a

正塩とは、酸と塩基が完全に中和して、酸の H⁺ や塩基の OH^－ が生成した塩に残っていないものをいいます。

1　酸の H₂SO₄ と塩基の Cu(OH)₂ が完全に中和して CuSO₄ という塩になっているので、正塩です。

2　酸の H₂SO₄ と塩基の NaOH が完全に中和して Na₂SO₄ という塩になっているので、正塩です。

3　H₂SO₄ は 2 価の酸なので、1 つの分子から 2 つの H⁺ が生じます。また NaOH は 1 価の塩基です。

H₂SO₄ が 1 mol と NaOH が 2 mol の比で反応するとき、完全に中和します。

NaHSO₄ は酸 H₂SO₄ と塩基 NaOH が中和した塩ですが、中和反応がまだ途中です。

H₂SO₄　+　NaOH　→　NaHSO₄　+　H₂O

という反応では、H₂SO₄ の H⁺ がまだ塩に残っています。

NaHSO₄　+　NaOH　→　Na₂SO₄　+　H₂O

まで反応が進むと、中和反応が完了します。

したがって H⁺ が残っているので、NaHSO₄ は酸性塩です。

4　NH₄Cl は H⁺ が残っているようにも見えますが、これは正塩です。

酸 HCl と塩基 NH₃ が中和してできた塩が NH₄Cl です。

HCl は 1 価の塩、NH₃ は 1 価の塩基であり、

HCl　+　NH₃　→　NH₄Cl

の反応で、中和は完了しています。

b

陽イオン交換樹脂から出てくる水素イオンの物質量は、問題文より

水素イオンの物質量　=　陽イオンの価数　×　陽イオンの物質量

となります。

ここではア～エは同じモル濃度・同じ体積なので、モル濃度を c mol/L 、体積を v L とおいて、ア～エで陽イオンの価数と陽イオンの物質量の積を比較します。

ア　KCl　→　K⁺　+　Cl^－

上のように水溶液中で電離するので、1 価　×　c [mol/L]　×　v [L]　=　cv [mol]

cv mol の K⁺ と交換されるので、cv mol の H⁺ が得られます。

イ　NaOH　→　Na⁺　+　OH^－

上のように水溶液中で電離するので、1 価　×　c [mol/L]　×　v [L]　=　cv [mol]

cv mol の Na⁺ と交換されるので、cv mol の H⁺ が得られます。

ただしこの場合は、水溶液中に同量の OH^－ が存在するので中和反応が起こり、

H⁺　+　OH^－　→　H₂O

となるので、H⁺ の物質量はかなり少なくなります。

ウ　MgCl₂　→　Mg²⁺　+　2 Cl^－

上のように水溶液中で電離するので、2 価　×　c [mol/L]　×　v [L]　=　2cv [mol]

2cv mol の H⁺ が得られます。

エ　CH₃COONa　→　CH₃COO^－　+　Na⁺

上のように水溶液中で電離するので、1 価　×　c [mol/L]　×　v [L]　=　cv [mol]

cv mol の Na⁺ と交換されるので、cv mol の H⁺ が得られます。

ただしこの場合は、水溶液中に同量の CH₃COO^－ が存在します。

酢酸 CH₃COOH は弱酸で一部の分子だけが電離しているので、

CH₃COO^－　+　H⁺　→　CH₃COOH

のような反応が起こり、H⁺ が酢酸の生成のために消費されるので、H⁺ の物質量は cv mol より少なくなります。

以上より、正解はウの③です。

問2　正解　a　2　　　b　2　　　c　1

a

CaCl₂ は強酸 HCl と強塩基 Ca(OH)₂ の塩であり、この塩の水溶液は中性です。

1　濃度が 0.100 mol/L の 2 価の強酸 H₂SO₄ 10.0 mL と、濃度が 0.100 mol/L の 1 価の強塩基　KOH を混合すると、

酸から H⁺ は　2 × 0.100 × \(\frac{10[mL]}{1000[mL]}\) mol 生じます。

塩基から OH^－ は　1 × 0.100 × \(\frac{10[mL]}{1000[mL]}\) mol 生じます。

酸が余るので、混合した水溶液は酸性です。

2　濃度が 0.100 mol/L の 1 価の強酸 HCl 10.0 mL と、濃度が 0.100 mol/L の 1 価の強塩基　KOH を混合すると、完全に中和します。

強酸と強塩基から生成した塩 KCl の水溶液となるので、水溶液は中性になります。

3　濃度が 0.100 mol/L の 1 価の強酸 HCl 10.0 mL と、濃度が 0.100 mol/L の 1 価の弱塩基　NH₃ を混合すると、完全に中和します。

強酸と弱塩基から生成した塩 NH₄Cl の水溶液となるので、水溶液は酸性になります。

4　濃度が 0.100 mol/L の 1 価の強酸 HCl 10.0 mL と、濃度が 0.100 mol/L の 2 価の強塩基　Ba(OH)₂ を混合すると、

酸から H⁺ は　1 × 0.100 × \(\frac{10[mL]}{1000[mL]}\) mol 生じます。

塩基から OH^－ は　2 × 0.100 × \(\frac{10[mL]}{1000[mL]}\) mol 生じます。

塩基が余るので、混合した水溶液は塩基性です。

b

「この実験は何の目的で行われるのか」を理解しましょう。

CaCl₂ は H₂O を吸収するので、実験室に放置された CaCl₂ がどれだけ H₂O を吸収しているのかを調べるのが、実験の目的です。

11.5 g の（ H₂O を吸収している）CaCl₂ を 50.0 mL の水に溶かすと

CaCl₂　→　Ca²⁺　+　2 Cl^－

のように電離するので、溶かした水溶液には Ca²⁺ 、Cl^－ 、50.0 mL の H₂O 、吸収していた H₂O が含まれます。

このうち Ca²⁺ を陽イオン交換樹脂により H⁺ と交換します。交換した H⁺ を塩酸としてすべて回収し、その一部を中和滴定します。

回収した塩酸を正確な一定量の溶液とし、その一部を中和滴定で正確な濃度を知ることで、H⁺ の全体量を計算できます。

そのため、得られたすべての塩酸をメスフラスコに移し、水を加えて一定量の溶液とします。したがって正解は②です。

＊＊＊＊＊

（＊＊＊で挟まれた文は、本問の解説を読み終わったあともう一度読み返してください。）

実験全体でみるとわかりますが、11.5 g の塩化カルシウムを 50.0 mL の水に溶かしていますが、50.0 mL という体積に意味はありません。別に 60 mL でも 100 mL でもかまいません。

もっと言えば、体積をはかる必要すらありません。約 50 mL の水に溶かしたなどで OK です。

重要なのは、溶かして陽イオン交換樹脂を詰めたガラス管に通し、さらに純水で洗い流した後に回収した溶液（ここでは塩酸）の体積を正確にメスフラスコではかる（ここでは 500 mL ）ことです。

純水でガラス管の中の陽イオン交換樹脂を洗い流すという操作があるので、溶かした水の体積はどうでもよいのです。

それより、Ca²⁺ をすべて H⁺ に交換して、ガラス管から回収した溶液（塩酸）の体積を正確にメスフラスコで一定量（ 500 mL ）に調製する、という操作が大切です。

回収した塩酸を正確な一定量の希釈溶液とし、さらにそこからホールピペットで正確にはかりとった希釈溶液を中和滴定することで、希釈溶液の濃度がわかり、塩酸全量の物質量がわかります。

塩酸全量の物質量がわかるので H⁺ の全物質量がわかり、交換した Ca²⁺ の物質量がわかるのです。

交換した Ca²⁺ の物質量がわかれば水に溶かす前の CaCl₂ の物質量がわかり、CaCl₂ の質量がわかります。

CaCl₂ の質量がわかれば、最後に 11.5 g との差から吸収した H₂O の質量がわかります。

＊＊＊＊＊

c

Ca²⁺ イオン 1 個が陽イオン交換樹脂にくっつくと、代わりに H⁺ イオンが 2 個放出されます。

さらに純水約 100 mL で洗い流します。これはガラス管内の陽イオン交換樹脂に残った Ca²⁺ と H⁺ を完全に交換するための操作です。

この洗い流す操作では、単に回収したビーカーの溶液（塩酸）に H₂O が増えるだけと考えてよいです。

ガラス管内を純水で洗い流したので、はじめのビーカーの水溶液中にあった Ca²⁺ は完全に H⁺ に置き換わりました。

また H⁺ イオンの物質量は Ca²⁺ の物質量の 2 倍になります。

500 mL にした希釈溶液からホールピペットで 10.0 mL とり、0.100 mol/L の NaOH 水溶液で中和滴定しました。この希釈溶液の濃度を C mol/L とすると、HCl は 1 価の酸、NaOH は 1 価の塩基なので、

$$1　×　C[mol/L]　×　\frac{10.0}{1000}[L]　=　1　×　0.100[mol/L]　×　\frac{40.0}{1000}[L]$$

これを解くと　C = 0.400 mol/L

希釈溶液の HCl の濃度が 0.400 mol/L とわかったので、この 500 mL に含まれる H⁺ の物質量は

0.400[mol/L]　×　\(\frac{500[mL]}{1000[mL]}\)　=　0.200[mol]

となります。

Ca²⁺ 1 mol 当たり H⁺ 2 mol と交換されているので、交換前の Ca²⁺ の物質量は 0.100 mol です。

CaCl₂　→　Ca²⁺　+　2 Cl^－

と電離するので、Ca²⁺ が 0.100 mol あれば CaCl₂ が 0.100 mol あったことになります。

CaCl₂ の式量は 111 なので、はじめの塩化カルシウムに CaCl₂ は

0.100[mol/L]　×　111[g/mol]　=　11.1[g]

含まれていました。

求める吸湿した水の質量は、

11.5[g]　－　11.1[g]　=　0.4[g]

となり、正解は①の 0.4 g です。

第1問

問1　正解　3

10 mL の生理食塩水には 35 mg のナトリウムイオン Na⁺ が含まれています。

そこで、1.0 L ( = 1000 mL )の生理食塩水には 3500 mg のナトリウムイオンが含まれることになります。

3500 mg = 3.5 g なので、ナトリウムイオンのモル質量 23 g/mol より、

求める 1.0 L の生理食塩水中のナトリウムイオンの物質量は

\(\frac{3.5[g]}{23[g/mol]}\) ≒ 0.15[mol]

問2　正解　1

1　×　純粋な水は融点と凝固点が 0 ℃なので、水は 0 ℃で凍ります。

しかし、水に何かが溶けている水溶液では、凝固点が 0 ℃より下がります。そのため、生理食塩水は 0 ℃より低い温度で凍ります。（例えば、海水は 0 ℃より低い温度で凍ります。）

また、純粋な水の沸点は 100 ℃なので、水は 100 ℃で沸騰します。しかし、水に何かが溶けている水溶液では、沸点は 100 ℃より高くなります。

2　〇　生理食塩水に含まれる塩化物イオン Cl^－ と硝酸銀水溶液の銀イオン Ag⁺ から、白色沈殿（塩化銀）が生じます。

Ag⁺　+　Cl^－　→　AgCl

3　〇　生理食塩水は塩化ナトリウムが溶けているので、電離して塩化物イオン Cl^－ とナトリウムイオン Na⁺ が等しい量だけ生じます。

NaCl　→　Na⁺　+　Cl^－

4　〇　ナトリウムイオンは黄色の炎色反応を示します。

問3　正解　6

実験結果より、コップⅢだけ BTB 溶液が青となりました。

BTB 溶液は、酸性 ( pH ＜ 6.0 ) で黄色、中性 ( pH = 6.0 ～ 7.6 ) で緑色、塩基性 ( pH ＞ 7.6 ) で青色です。

飲料水 X は pH = 8.8～9.4 なので、コップⅢが飲料水 X です。

実験結果より、コップⅠだけ電球がつきました。

電気を通すために、コップⅠにはイオンが多く含まれる飲料水が入っています。

最も多くイオンを含んでいる飲料水は Z です。そこで、コップⅠは飲料水 Z です。

問4　正解　7

a　ナフタレンが主成分の防虫剤は、時間とともに固体のナフタレンが昇華して気体となります。そのため、時間が経過すると固体のナフタレンは小さくなり、防虫剤も小さくなります。

b　ティーバッグ内の紅茶成分が、お湯に浸すことによって溶け出します。このように、ある物質が溶けやすい溶媒に溶けて分離されることを抽出といいます。

c　沸点の差を利用して、加熱して集めたい成分だけを分離する操作を蒸留といいます。

問5　正解　6

銅 Cu は電気や熱の伝導性が高く、導線に使用されます。

鉄 Fe は建造物の鉄骨や鉄筋として、構造材料に使われます。

アルミニウム Al は密度が小さい軽い金属です。飲料用の缶やサッシ、1 円硬貨などに使われます。

第2問

問1　正解　3

H₂O では H－O 結合の共有電子対が酸素原子側に引きつけられるので、水素原子が +1 です。（酸素原子の酸化数は －2 ）

CH₄ では H－C 結合の共有電子対が炭素原子側に引きつけられるので、水素原子が +1 です。（炭素原子の酸化数は －4 ）

H₂ では H－H 結合の共有電子対に偏りはないので、水素原子の酸化数は 0 です。

したがって、酸化数が +1 となる原子をもつのは H₂O と CH₄ です。

また H₂O と CH₄ の分子のうち、分子全体で無極性となるのは 正四面体形の CH₄ です。

H₂O は折れ線形のため、分子全体で極性をもちます。

まとめると、酸化数が +1 の原子を含む無極性分子は CH₄ のみです。

問2　正解　A　6　　　　　B　3

炭素原子 A

炭素原子 A の酸化数を数えます。炭素原子 A には、4 つの共有結合があります。

C－C 結合に共有電子対の偏りはありません。

C－H 結合では、共有電子対の電子を炭素原子が引きつけます。これより酸化数は －1 × 2 = －2

C－O 結合では、共有電子対の電子を酸素原子が引きつけます。これより酸化数は +1

以上を合計すると、－2 + (+1) = －1

したがって炭素原子 A の酸化数は －1 です。

炭素原子 B

炭素原子 B の酸化数を数えます。炭素原子 B には、4 つの共有結合があります。

C－C 結合に共有電子対の偏りはありません。

C＝O 結合では、共有電子対の電子を酸素原子が引きつけます。これより酸化数は +1 × 2 = +2

C－O 結合では、共有電子対の電子を酸素原子が引きつけます。これより酸化数は +1

以上を合計すると、+2 + (+1) = +3

したがって炭素原子 B の酸化数は +3 です。

問3　正解　4

問題で与えられた2つの半反応式について

C₆H₈O₆ 　→　C₆H₆O₆　+　2 H⁺　+　2 e^－　　‥‥(1)

O₂　+　4 H⁺　+　4 e^－　→　2 H₂O　　‥‥(2)

(1) × 2 + (2) を計算して電子を消去します。

2 C₆H₈O₆　+　O₂　→　2 C₆H₆O₆　+　2 H₂O

となるので、2 mol のビタミン C と 1 mol の酸素が反応することがわかります。

グラフ④では 1.0 mol のビタミン C と 0.5 mol の酸素が反応しているので、反応の比率が該当します。

第3問

問1　正解　4

塩化水素 HCl は 1 価の強酸、水酸化ナトリウム NaOH は 1 価の強塩基です。

そこで、試料を希釈した溶液の塩化水素のモル濃度を C mol/L として、これを 10 mL はかりとったとします。この溶液を 0.1 mol/L の水酸化ナトリウム水溶液 15 mL で中和すると考えます。

C[mol/L] × 1価 × \(\frac{10[mL]}{1000[mL]}\) = 0.1[mol/L] × 1価 × \(\frac{15[mL]}{1000[mL]}\)

これを解くと C = 0.15[mol/L]

これより、試料の HCl モル濃度の約 3 mol/L を、0.15 mol/L まで希釈したいことがわかります。

\(\frac{0.15[mol/L]}{3[mol/L]}\) = \(\frac{1}{20}\)

試料のモル濃度を 20 分の 1 にしたいので、20 倍に希釈します。

問2　正解　4

水酸化ナトリウム水溶液の滴下量が正しい量より大きくなるということは、実験操作の途中で酸が混入している可能性があります。つまり、試料がどこかの段階で混入していると思われます。

あるいは、何らかの理由で中和点に気付かずに水酸化ナトリウム水溶液を滴下しすぎた、実験操作のどれかで正確に値を読み取っていない、などの原因も考えられます。

1　×　試料をはかりとるホールピペットが水でぬれている場合は、試料が薄まるので酸の量が減り、水酸化ナトリウム水溶液の滴下量は小さくなります。

2　×　コニカルビーカーが水でぬれていても試料の量は変わらないので、水酸化ナトリウム水溶液の滴下量は正しくなります。

3　×　フェノールフタレイン溶液を多量に加えると、変色域が酸性側に移動すると考えられます。そのため、水酸化ナトリウム水溶液を滴下すると、正しい量より少ない時点で変色すると思われます。

4　〇　ビュレット内の空気が滴定中に抜けるということは、ビュレットの液面の目盛りが下がります。

水酸化ナトリウム水溶液を実際に滴下した量よりも液面の目盛りが下がるので、より多くの量を滴下したと見えてしまいます。

（実際には正しい量の水酸化ナトリウム水溶液を滴下しましたが、空気の体積分だけ滴下量を大きく記録してしまったことになります。）

問3　正解　2

密度が 1.04 g/cm³ と測定できたので、試料 10 mL (= 10 cm³) の質量は

1.04[g/cm³] × 10[cm³] = 10.4[g]

モル濃度が 2.60 mol/L なので、10 mL の試料に含まれる塩化水素 HCl の物質量は

2.60[mol/L] × \(\frac{10}{1000}\)[L] = 0.0260[mol]

HCl の分子量は 36.5 であるから、物質量が 0.0260mol のHCl の質量は

36.5[g/mol] × 0.0260[mol] = 0.949[g]

これらより、求める質量パーセント濃度は

\(\frac{0.949[g]}{10.4[g]}\) × 100 ≒ 9.13[%]

となります。

問4　正解　3

次亜塩素酸ナトリウム NaClO は、弱酸である次亜塩素酸 HClO と強塩基である水酸化ナトリウム NaOH の塩です。

(1)の式では、弱酸の塩に強酸である塩酸 HCl を加えることで、弱酸の HClO が遊離して強酸の塩 NaCl が生成しています。

【反応】あ

過酸化水素水に酸化マンガン(Ⅳ)を加えると、酸素が発生します。

2 H₂O₂　→　2 H₂O　+　O₂

酸化マンガン(Ⅳ)は触媒としてはたらいていて、反応式には出てきません。

この反応は過酸化水素の分解反応（酸化還元反応）であり、酸化マンガン(Ⅳ)は反応を速く進めるために加えられています。

【反応】い

酢酸ナトリウムは弱酸の塩であり、強酸である希硫酸を加えると弱酸である酢酸が遊離して、酢酸のにおいである刺激臭がします。

2 CH₃COONa　+　H₂SO₄　→　2 CH₃COOH　+　Na₂SO₄

【反応】う

亜鉛 Zn に希塩酸 HCl を加えると水素が発生します。

Zn　+　2 HCl　→　ZnCl₂　+　H₂

亜鉛原子が酸化され、水素原子が還元される酸化還元反応です。

【反応】あ～うでは、いが弱酸の遊離反応で、あとうが酸化還元反応です。式(1)と類似性の高い反応はいです。

第1問

問1　正解　4

原子の電子配置は、一般に内側の電子殻から順番に電子が入っていきます。

またイオンの電子配置は、もとの原子に最も近い希ガスの電子配置と同じになります。

1　〇　炭素原子は原子番号 6 で、電子の数は 6 個です。K 殻に 2 個、L 殻に 4 個の電子があります。

2　〇　硫黄原子は原子番号 16 で、電子の数は 16 個です。電子は K 殻に 2 個、L 殻に 8 個、M 殻に 6 個入ります。最外殻の電子数が 6 個なので、価電子は 6 個です。

3　〇　ナトリウム原子の原子番号は 11 で、電子は 11 個あります。1 価の陽イオンであるナトリウムイオン Na⁺ は電子を 1 個失っており、電子を 10 個持ちます。

フッ素原子は原子番号 9 で、電子を 9 個持ちます。1 価の陰イオンであるフッ化物イオン F^－ は電子を 1 個受け取っており、電子を 10 個持ちます。

このように、ナトリウムイオンとフッ化物イオンの電子数はどちらも 10 個で、同じ電子配置になります。

なお電子を 10 個もつ原子は、それぞれの原子と近い大きさである希ガスのネオン Ne です。

4　×　窒素とリンはどちらも 15 族の元素です。最外殻の電子数はどちらも 5 個です。

窒素原子は原子番号 7 で、電子を 7 個持ちます。電子配置は K 殻に 2 個、L 殻に 5 個です。

リン原子は原子番号 15 で、電子を 15 個持ちます。電子配置は K 殻に 2 個、L 殻に 8 個、M 殻に 5 個です。

問2　正解　3

オの部分は典型元素です。

3 族から 11 族の範囲が遷移元素です。それ以外の 1 ～ 2 族、12 ～ 18 族は典型元素です。（ 12 族を遷移元素に含めるものもあります。）

1　〇　1 族と 2 族は典型元素です。

2　〇　3 ～ 11 族は遷移元素です。

3　×　12 ～ 15 族はすべて典型元素です。

4　〇　13 ～ 16 族はすべて典型元素です。

5　〇　17 族は典型元素で、ハロゲンと呼ばれます。18 族は典型元素で、希ガスと呼ばれます。

問3　正解　2　5

これらの分子内には原子同士の共有結合である O－H 結合、C＝O 結合、N－H 結合、C－O 結合、C－H 結合があります。この 5 つの共有結合にはすべて極性があります。

そこで、分子全体として極性が打ち消されるものを選びます。

1　×　H₂O は折れ線形の分子のため、O－H 結合の極性が打ち消されないので、分子全体で極性があります。

2　〇　CO₂ は直線形の分子のため、C＝O 結合の極性が逆向きとなって打ち消され、分子全体では極性はありません。

3　×　NH₃ は三角錐形なので、N－H 結合の極性が打ち消されません。そのため、分子全体で極性があります。

4　×　C₂H₅OH は立体的に折れ曲がった構造です。C－H 結合、C－O 結合、O－H 結合それぞれに極性があり、これらの極性は打ち消されないので、分子全体でも極性があります。

5　〇　CH₄ は正四面体形の分子であり、C－H 結合の極性がすべて正四面体の中心に向いています。そのため分子全体では、極性が打ち消されて極性はありません。

選択肢 3 の図を参照してください。

問4　正解　2

1　〇　沸点以下の温度でも、液体は液面から蒸発してゆっくりと気体になっています。

2　×　ヨウ素 I₂ や二酸化炭素（ドライアイス） CO₂ は、気体から固体に、また固体から気体に状態変化します。気体から固体、固体から気体への状態変化は昇華と言います。

3　〇　一定温度でも、気体分子の速度にはばらつきがあります。空間を速く飛びまわる分子も、ゆっくり動く分子もあります。

温度が高くなると気体分子の動きは活発になるので、気体分子の平均の速度は速くなります。

4　〇　分子は、気体・液体・固体のどの状態でも熱運動をしています。固体の分子結晶では分子の位置が決まっているので、分子はその位置で振動しています。

問5　正解　5

蒸留操作で沸点を測定するときは、温度計の下端部を枝付きフラスコの分岐する高さに合わせます。

これは冷却器の方向へ流れる気体の温度を正確に測るためです。

蒸留操作では、三角フラスコで集めた液体が何であるか確かめたいです。そのために、この液体の沸点を測定しておきます。

純物質は沸点が正確に決まっているので、それと比較して集めた液体が目的とする物質なのかを確認することができます。

この実験では蒸留水を集めることを目的としているので、加熱して沸騰したときに温度計が 100 ℃を示していれば、蒸留水が得られていると推測できます。

以上より、手順Ⅰに関する注意点の選択肢は　ウ　です。

次に、アダプターと三角フラスコの接続部をどうするかという設問です。

アダプターと三角フラスコをゴム栓でつないで密閉すると、加熱により実験装置内の圧力が高まって危険です。

実験装置を密閉して加熱すると、ガラス器具が割れたり、接続部分のゴム栓が吹き飛んだりする恐れがあります。

そこでこの実験では、異物が三角フラスコに入らないようにアルミ箔で覆うだけにとどめます。

したがって、手順Ⅱに関する注意点の選択肢は　エ　です。

問6　正解　4

得られた CaSO₄・2 H₂O の物質量は、\(\frac{8.6[g]}{172[g/mol]}\) = 0.050[mol]です。

この沈殿は、水溶液中の Ca²⁺ イオンと SO₄^2－ イオンから生成します。そのため十分な量の硫酸ナトリウムがある場合、Ca²⁺ イオン 1 mol から CaSO₄・2 H₂O の沈殿が 1 mol 得られます。

また、CaBr₂ は水溶液中で以下のように電離します。

CaBr₂　　→　　Ca²⁺　+　2 Br^－

そのため、CaBr₂ を 1 mol 溶かすと、2 mol の臭化物イオン Br^－ が水溶液中に存在します。

したがって、水溶液中の臭化物イオン Br^－ が 0.024 mol 存在したということは、CaBr₂を 0.012 mol 溶解させたとわかります。

CaBr₂ を 0.012 mol 溶かすと、CaSO₄・2 H₂O は 0.012 mol 沈殿します。

したがって沈殿物のうち 0.050[mol] – 0.012[mol] = 0.038[mol] が、CaCl₂ から生成したものです。

問7　正解　1

1　×　ボーキサイトの主成分は Al₂O₃・nH₂O です。製錬されるアルミニウムの原料となるのがボーキサイトです。

ガラス、シリカゲル、石英、ケイ砂、水晶などの原料となるのが二酸化ケイ素です。

2　〇　塩素を水に溶かすと次亜塩素酸 HClO が生成します。次亜塩素酸には殺菌、漂白作用があります。

Cl₂　+　H₂O　　→　　HCl　+　HClO

3　〇　エチレン C₂H₄ が連続的に反応してできた高分子がポリエチレンです。

4　〇　白金はイオン化傾向がとても小さいので、反応性に乏しい金属です。このように、白金や金は安定した金属元素です。

第2問

問1　正解　5

原子の質量数の総和 M が 70 となる塩素分子は、質量数 35 の塩素原子と質量数 35 の塩素原子が共有結合してできたものです。

同様に、原子の質量数の総和 M が 72 となる塩素分子は、質量数 35 の塩素原子と質量数 37 の塩素原子が共有結合してできたものです。

同様に、原子の質量数の総和 M が 74 となる塩素分子は、質量数 37 の塩素原子と質量数 37 の塩素原子が共有結合してできたものです。

質量数 35 の塩素原子は 76 ％の比率で存在しているので、質量数の総和 M が 70 の塩素分子となる割合は 76% × 76% ≒ 58% です。

問2　正解　1

モル濃度が 0.25 mol/L で 200 mL ( = 0.200 L ) の NaNO₃ 水溶液には、NaNO₃ が

0.25[mol/L] × 0.200[L] = 0.050[mol]

含まれます。

これから調製したい（つくりたい）、モル濃度が 0.12 mol/L で 500 mL ( = 0.500 L ) の NaNO₃ 水溶液について考えます。

この調製したい NaNO₃ 水溶液には、NaNO₃ が

0.12[mol/L] × 0.500[L] = 0.060[mol]

含まれているはずです。

そのため、加えなければならない NaNO₃ の物質量は

0.060[mol] － 0.050[mol] ＝ 0.010[mol]

です。

また、NaNO₃ の式量（モル質量 [g/mol] ）は、23 + 14 + 16 × 3 = 85 です。

したがって、加える NaNO₃ の質量は

85[g/mol] × 0.010[mol] = 0.85[g]

となります。

問3　正解　A　8　　　　　B　4

問題の選択肢から水溶液 A と B について、1 価の強酸である塩酸、1 価の弱酸である酢酸、1 価の強塩基である水酸化ナトリウムの可能性を考えます。

滴定曲線のグラフを見ると、pH 12（強塩基の領域）から、水溶液 B を 15 mL 滴下したところで pH 7 よりは塩基性側で中和して、pH 4～5（弱酸の領域）に至っています。

滴定開始前に pH = 12 ということは、水素イオン濃度 [H⁺] は 1.0 × 10^－12 mol/L です。

水のイオン積

Kw　=　[H⁺] [OH^－]　=　1.0 × 10^－14 mol²/L²

より、

[OH^－] = 1.0 × 10^－2 mol/L になります。

最初に pH = 12 なので、水溶液 A として、0.01 mol/L の強塩基がビーカーに入っていたとわかります。これに当てはまるのは、0.010 mol/L の水酸化ナトリウムです。

この塩基 150 mL を水溶液 B 15 mL で中和しています。

水溶液 B は塩酸か酢酸のどちらかですが、いずれも 1 価の酸なので、酸の濃度は塩基の 10 倍だとわかります。

したがって、酸の濃度は 0.10 mol/L です。

さらに、中和点が弱塩基性であること、中和反応後に酸を加え続けると溶液が弱酸性になることから、この酸は弱酸と考えられます。

したがって、水溶液 B は 0.10 mol/L 酢酸水溶液とわかります。

問4　正解　3

ア～ウは、酸と塩基の中和反応でできた塩です。

中和反応で生成する塩を水に溶かすと、その液性は塩によって決まります。

ア　塩化ナトリウム NaCl は、強酸の塩化水素（塩酸） HCl と強塩基の水酸化ナトリウム NaOH からできた塩です。

この塩を水に溶かすと中性であり、pH 7 となります。

イ　炭酸水素ナトリウム NaHCO₃ は、弱酸の炭酸 H₂CO₃ と強塩基の水酸化ナトリウム NaOH からできた塩です。

NaHCO₃ の水溶液では、炭酸水素イオン HCO₃^－ とナトリウムイオン Na⁺ が存在します。

このうち Na⁺ はイオンのまま存在しますが、炭酸水素イオン HCO₃^－ は一部が H⁺ を受け取り塩基として働きます。

HCO₃^－　+　H₂O　→　H₂CO₃　+　OH^－

NaHCO₃ 水溶液では水酸化物イオン OH^－ が生じるので、この水溶液は弱塩基性を示します。

したがって pH は 7 より大きくなります。

ウ　硫酸水素ナトリウム NaHSO₄ は、強酸の硫酸 H₂SO₄ と強塩基の水酸化ナトリウム NaOH からできた塩です。

NaHSO₄ の水溶液には、硫酸水素イオン HSO₄^－ とナトリウムイオン Na⁺ が存在します。

このうち Na⁺ はイオンのまま存在しますが、硫酸水素イオン HSO₄^－ の一部はさらに H⁺ を放出して酸として働きます。

HSO₄^－　→　H⁺　+　SO₄^2－

NaHSO₄ 水溶液では水素イオン H⁺ が生じるので、この水溶液は弱酸性を示します。

したがって pH は 7 より小さくなります。

まとめると pH が大きい順に

NaHCO₃ 水溶液 ＞ NaCl 水溶液 ＞ NaHSO₄ 水溶液

問5　正解　2

1　〇　酸化還元反応で発生する化学エネルギーを電気エネルギーに変えるのが電池です。

2　×　電池の放電時には、負極で酸化反応が起こり電子が放出され、この電子が正極に移動して還元反応が起こります。

このとき電流は、正極から負極へと流れます。

3　〇　正しい記述です。

4　〇　水素を燃料とする燃料電池の反応では、水素と酸素から水が生成します。

負極の活物質に水素 H₂ 、正極の活物質に酸素 O₂ が用いられます。

負極では H₂ が電子を放出して H⁺ となります。この H⁺ が正極で酸素 O₂ と還元反応をして、水 H₂O が生成します。

負極の反応は　　H₂　→　2 H⁺　+　2 e^－　　です。

正極の反応は　　O₂　+　4 H⁺　+　4 e^－　→　2 H₂O　　です。

電池全体の反応は　　2 H₂　+　O₂　→　2 H₂O　　です。

問6　正解　1

イオン化傾向の大きさと、溶液の性質（酸化力）を見て判断します。

1　〇　硝酸銀 AgNO₃ 水溶液には、銀イオン Ag⁺ と硝酸イオン NO₃^－ が存在します。

鉄 Fe は銀 Ag よりもイオン化傾向が大きいので、鉄が溶けて陽イオンとなり、陽イオンだった銀が析出します。

2 Ag⁺　+　Fe　→　2 Ag　+　Fe²⁺

2　×　硫酸銅(Ⅱ) CuSO₄ 水溶液には、銅イオン Cu²⁺ と硫酸イオン SO₄^2－ が存在します。

水溶液中には水素イオン H⁺ も存在しますが、H と Cu では Cu の方がイオン化傾向が小さいので、H⁺ は陽イオンのままで水溶液中に残ります。

そのため、H⁺ が電子を受け取って、水素が発生することはありません。

亜鉛が溶けて、水素よりイオン化傾向の小さい銅イオン Cu²⁺ が電子を受け取り析出します。

Zn　+　Cu²⁺　→　Zn²⁺　+　Cu

3　×　希硝酸は酸化力が強いので銅を溶かします。

希硝酸と銅の半反応式は以下の通りです。

HNO₃　+　3 H⁺　+　3 e^－　　→　　NO　+　2 H₂O

Cu　　→　　Cu²⁺　+　2 e^－

この 2 つの半反応式から電子を消去して整理すると、

3 Cu　+　8 HNO₃　　→　3 Cu(NO₃)₂　+　2 NO　+　4 H₂O

反応式からわかるように、水素は発生せず、一酸化窒素が発生します。

4　×　アルミニウムは濃硝酸に溶けますが、溶け始めると表面が酸化被膜で覆われます（不動態）。

酸化被膜は濃硝酸に溶けないので、アルミニウム板が溶け続けることはありません。

第1問

問1　正解　4

それぞれの分子の構造式は以下の通りです。

分子内の共有結合を数えると、NH₃ は 3 個、HCN は 4 個、CH₃OH は 5 個、C₂H₄ は 6 個です。

このように、共有結合に使われている電子の総数が最も多いのは、エチレン C₂H₄ です。

なお、1 つの共有結合は 2 個の電子でつくられているので、C₂H₄ では 12 個の電子が共有結合に使われています。

そのほかの分子では、 NH₃ は 6 個、HCN は 8 個、CH₃OH は 10 個の電子が共有結合に使われています。

問2　正解　1

1　×　同位体は陽子の数が等しく（つまり原子番号は同じです）、中性子の数が異なります。

2　〇　同位体は中性子の数が異なります。中性子の数が異なるので質量数が違います。

3　〇　中性子は化学反応にほとんど関係ないので、中性子の数が異なっても化学的性質はほぼ同じです。

4　〇　記述のとおり、放射線を放出して原子が崩壊し、放射性同位体の量が半分に減るまでの時間を半減期といいます。

問3　正解　4

1　〇　同じ周期の元素では、原子番号が 1 大きくなると、最外殻電子数は 1 増えます。

2　〇　He は最外殻の電子数が 2 個、Ne と Ar は最外殻の電子数が 8 個で、価電子は 0 個となります。

3　〇　第 2 周期と第 3 周期の同族の元素では原子番号が 8 ずれているので、陽子数の差は 8 個です。

4　×　イオン化エネルギーは、電子 1 個を取り去るために必要なエネルギーです。イオン化エネルギーは、周期表の左下の元素が小さい傾向です。

原子核（陽子）から遠い位置にある電子の方が、近い位置にある電子より離れやすいので、同族元素では原子番号が大きいとイオン化エネルギーは小さくなります。

問4　正解　3

1　〇　金属は展性（叩いて薄く広げられる）や延性（引っ張って細く伸ばせる）という性質を持ちます。

2　〇　共有結合は強固なので、共有結合が切れて水に溶けるということは起こりにくいです。

ダイヤモンドや黒鉛、水晶など共有結合結晶の例を思い浮かべると、水に溶けにくいと判断できます。

3　×　イオン結晶は固体の状態では電気を通しにくいです。イオン結晶を溶液に溶かすか、融解させて液体の状態にすると、電気を通します。

4　〇　分子結晶は結合する力が弱いので、結晶も柔らかくなります。

問5　正解　3

水溶液の密度が 1.2[g/cm³] で 50[mL] あるので、この水溶液の質量は

1.2[g/cm³] × 50[cm³] = 60[g] です。

質量パーセント濃度が 20 % なので、この水溶液に溶けている MgCl₂ の質量は

60[g] × \(\frac{20}{100}\) = 12[g] です。

MgCl₂ のモル質量は 24 + 35.5 × 2 = 95[g/mol] となります。

したがって、水溶液中の MgCl₂ の物質量は

\(\frac{12[g]}{95[g/mol]}\) ≒ 0.126[mol] です。

MgCl₂を 1 mol 溶かすと水溶液中の塩化物イオン Cl^－ は 2 mol となるので、求める塩化物イオンの物質量は

0.126[mol] × 2 ≒ 0.25[mol] です。

問6　正解　1

1　×　炭素原子は 4 つの共有結合をもち、ダイヤモンドでは正四面体形の構造が繰り返されます。

2　〇　炭素原子が球状に結合した物質をフラーレンといいますが、これは炭素の同素体です。

3　〇　黒鉛では隣接する 3 つの炭素原子と共有結合します。そのため、結合する角度が 120 度の平面上の構造となり、正六角形の構造が繰り返されます。

4　〇　黒鉛は電気を通します。

問7　正解　ア　1　　　　　イ　5

6 種類の純物質のうち、水に溶けてろ液に含まれるのは 2 種類です。

塩化カリウム KCl 、炭酸水素ナトリウム NaHCO₃ が溶けます。

他の炭酸カルシウム CaCO₃ 、硫酸バリウム BaSO₄ 、鉄 Fe 、銅 Cu は水に溶けずに固体のままです。

実験Ⅰでは金属の炎色反応を調べています。

カリウムイオンは赤紫色、ナトリウムイオンは黄色です。炎の色が赤紫色なので、アは塩化カリウムと考えられます。

実験Ⅱについて、塩化カリウム以外の 5 種類の純物質との反応を考えます。

(a)　炭酸水素ナトリウム NaHCO₃ に塩酸を加えると、二酸化炭素が発生します。

NaHCO₃　+　HCl　　→　　NaCl　+　H₂O　+　CO₂

二酸化炭素は空気より重く、水に少し溶け、燃焼しません。

(b)　炭酸カルシウム CaCO₃ に塩酸を加えると、二酸化炭素が発生します。

CaCO₃　+　2 HCl　　→　　CaCl₂　+　H₂O　+　CO₂

(c)　硫酸バリウム BaSO₄ に塩酸を加えても反応しません。

(d)　鉄 Fe に塩酸を加えると、水素が発生します。

Fe　+　2 HCl　→　FeCl₂　+　H₂

水素は無色無臭で空気より軽く、水にほとんど溶けず、爆発的に燃焼します。したがってイは鉄です。

(e)　銅 Cu に塩酸を加えても反応しません。硝酸など酸化力のある酸に溶けます。

第2問

問1　正解　3

アスコルビン酸の分子量（モル質量 g/mol ）は、12 × 6 + 1.0 × 8 + 16 × 6 = 176

500 mL ( = 0.500 L ) に 0.88 g 含まれているので、求めるモル濃度は

$$\frac{0.88[g]}{176[g/mol]} \times \frac{1}{0.500[L]} = 0.010 [mol/L]$$

問2　正解　2

ナトリウムと水の反応は

2 Na　+　2 H₂O　→　2 NaOH　+　H₂

となるので、2 mol のナトリウムと 2 mol の水が反応すると、1 mol の水素が発生します。

ナトリウムは \(\frac{0.92[g]}{23[g/mol]}\) = 0.040[mol] 存在します。

水は \(\frac{90[g]}{18[g/mol]}\) = 5.0[mol] 存在します。

水は十分あるので、ナトリウム全量と反応します。このとき水素は 0.020 mol 発生します。

水素の分子量は 2.0 なので、求める質量は 2.0[g/mol] × 0.020[mol] = 0.040[g] です。

問3　正解　5

1　〇　ブレンステッド・ローリーの定義では、水溶液中に限らず、気体状態でも水素イオンのやり取りを考えることができます。

例えばアンモニア水の入った試験管の口に、濃塩酸を付着させたガラス棒を近づけると、白煙が生じます。

これは気体となったアンモニア NH₃ と、ガラス棒の先で気体となった塩化水素 HCl が反応し、塩化アルミニウム NH₄Cl の微粒子が生成するためです。

結果として、NH₄Cl の微粒子のまとまりが白い煙のように見えます。これは酸塩基反応です。

2　〇　弱酸の塩に強酸を加えると、弱酸が遊離します。

（例：酢酸ナトリウム CH₃COONa に塩酸 HCl を加えると、酢酸が遊離します。）

CH₃COONa　+　HCl　→　NaCl　+　CH₃COOH

3　〇　酸の価数 × 酸の物質量 = 塩基の価数 × 塩基の物質量 が成り立つのが中和点です。

4　〇　純粋な水では、

H₂O　→　H⁺　+　OH^－

と電離している以外にイオンは存在しないので、

[H⁺] = [OH^－]

となります。

5　×　塩基の価数と塩基の強弱は関係ありません。

問4　正解　2

pHは、[H⁺] = 1.0 × 10^－pH mol/L と定義されます。

水素イオン濃度が高いほど、pHは小さくなります。

塩酸は強酸なので、水溶液中では完全に電離します。そのため、

アの水素イオン濃度は 0.010 mol/L = 1.0 × 10^－2 mol/L (pH = 2)

イの水素イオン濃度は 0.0010 mol/L = 1.0 × 10^－3 mol/L (pH = 3)です。

酢酸は弱酸なので、水溶液中の一部の酢酸分子だけが電離して、水素イオンを生成します。

CH₃COOH　⇄　CH₃COO^－　+　H⁺

ウは電離度 0.020 なので、

水素イオン濃度は 0.10 × 0.020 = 0.0020 = 2.0 × 10^－3 mol/L (pH ≒ 2.7)

水素イオン濃度が高いと pH は小さいので、pH の小さい順に ア ＜ ウ ＜ イ となります。

問5　正解　2

半反応式は次の通りです。

MnO₂　+　2 e^－　+　4 H⁺　→　Mn²⁺　+　2 H₂O

2 Cl^－　→　Cl₂　+　2 e^－

この 2 式を加えると

MnO₂　+　2 Cl^－　+　4 H⁺　　→　　Mn²⁺　+　2 H₂O　+　Cl₂

2Cl^－ を両辺に加えて反応式を完成させると

MnO₂　+　4 HCl　　→　　MnCl₂　+　2 H₂O　+　Cl₂

この酸化還元反応では、Mn 1 mol と電子 2 mol 、また Cl₂ 1 mol と電子 2 mol が反応しています。

そこで、0.25 mol の Cl₂ が発生したとき、 Mn が受け取る電子は 0.50 mol です。

問6　正解　2

ア

過酸化水素は酸化剤として作用しています。

半反応式は次の通りです。

H₂O₂　+　2 H⁺　+　2 e^－　→　2 H₂O

H₂S　→　S　+　2 H⁺　+　2 e^－

これらの 2 式を加えてできる反応式は

H₂O₂　+　H₂S　→　S　+　2 H₂O

となります。このとき水溶液中で生成した S のために白濁します。

イ　

ヨウ化カリウムは還元剤として作用しています。

半反応式は次の通りです。

H₂O₂　+　2 H⁺　+　2 e^－　→　2 H₂O

2 I^－　→　I₂　+　2 e^－

これらの 2 式を加えてできるイオン反応式は

H₂O₂　+　2 H⁺　+　2 I^－　　→　　2 H₂O　+　I₂

両辺に 2 K⁺ と SO₄^2－ を加えて式を整理すると

H₂O₂　+　H₂SO₄　+　2 KI　→　I₂　+　2 H₂O　+　K₂SO₄

となります。

このとき水溶液中で生成したヨウ素 I₂ とヨウ化物イオン I^－ から、三ヨウ化物イオン I₃^－ が生じます。

この三ヨウ化物イオンにより、水溶液の色が褐色となります。

ウ

二酸化炭素は酸化剤として作用しています。

二酸化炭素分子のなかの炭素原子が還元されて単体となることで、黒色の炭素が生成します。

CO₂　+　2 Mg　→　C　+　2 MgO

二酸化炭素はマグネシウムに酸素を与えています。このとき CO₂ の炭素原子の酸化数は +4 から 0 へ変化しています。