各原子の質量は、相対質量で表します。
相対質量は、質量数 12 の炭素原子 12C を基準として、これとの比で算出します。
同位体が存在する元素の原子の質量は、原子量で表します。
原子量とは、それぞれの同位体の相対質量に存在比をかけて、求めた平均値のことです。
分子量は、その分子を構成しているすべての原子の原子量を、すべて足し合わせた値です。
イオン結晶や金属結晶などは組成式で表されます。このような化合物では、組成式で表された原子の原子量の総和を考えます。これを式量といいます。
もくじ
相対質量
一般に化学では、物質同士の関係を、最も簡単な整数比で表して考えます。
例えば、2 個の水素原子 H と 1 個の酸素原子 O が反応すると、1 個の水分子 H2O になります。
また、1 個のメタン分子 CH4 は、4 個の水素原子 H と 1 個の炭素原子 C からできています。
このメタン分子 CH4 1 個を 2 個の酸素分子 O2 を反応させると、1 個の二酸化炭素分子 CO2 と 2 個の水分子 H2O になります。
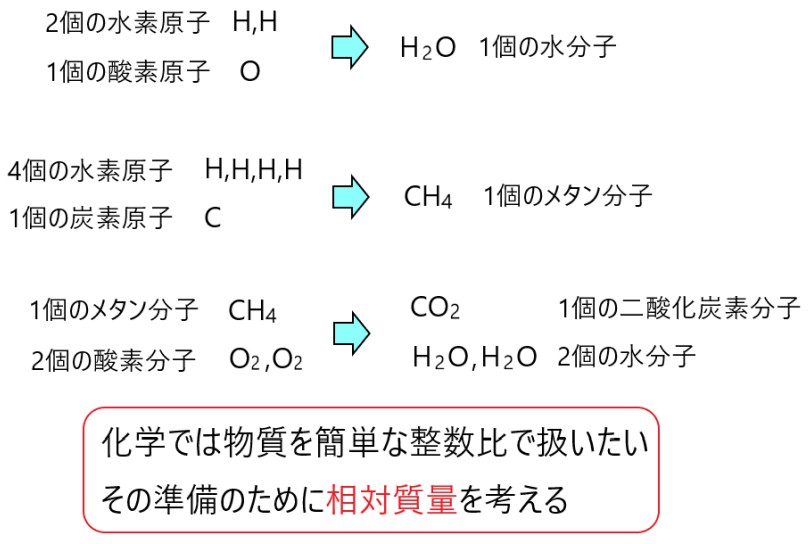
原子や分子といった粒子は非常に小さく、取り扱いにくいものです。これらの反応などを考えるときは、原子や分子を簡単な整数比で扱うと、理解しやすくなります。
それぞれの原子や分子、イオンなどを比で表す準備として、相対質量を考えます。
各原子の質量を考えるとき、質量数 12 の炭素原子 12C を基準とします。
「質量数 12 の炭素原子 12C 1 個の質量を 12 とする」と定め、他の原子の質量はこれとの比で表します。この比の値を、原子の相対質量といいます。
相対質量は質量の比であるので、単位はありません。
「質量数 12 の炭素原子 12C 1 個の質量を 12 とする」ので、例として質量数 1 の水素原子 1H 1 個の相対質量はいくらか、計算しましょう。
具体的には、炭素原子 12C 1 個の質量は 1.9926 × 10－23 [g] であり、水素原子 1H 1 個の質量は 0.16735 × 10－23 [g] です。
水素原子 1H の相対質量を X とします。相対質量は比ですから、炭素原子 12C の質量との比から X を求めます。
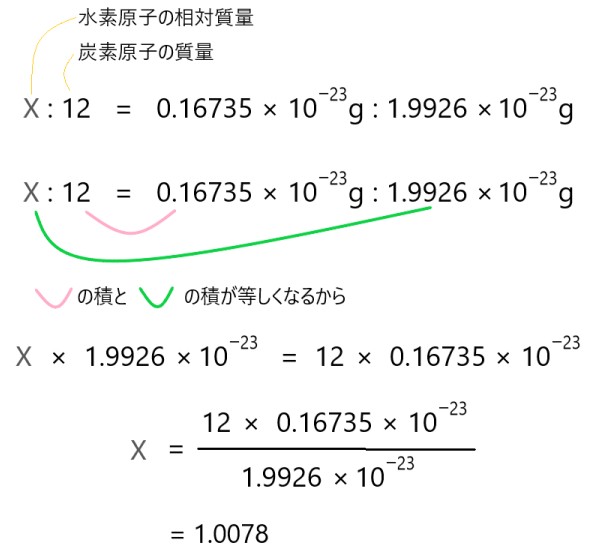
以上のように比を計算すると、X = 1.0078 と水素原子 1H の相対質量が求まります。
ところで原子の質量数を考えたとき、陽子と中性子はほぼ同じ重さであり、電子はそれらより非常に小さい重さでした。そのため、質量数は陽子と中性子の和と定めていました。
相対質量を考えるとき、陽子数が 6 個で中性子数が 6 個、電子数が 12 個の炭素原子 12C を基準としています。
これに対して、水素原子 1H は陽子数が 1 個で電子数が 1 個でした。
重い陽子と中性子だけで表す質量数は12C が 12 であり、1H の質量数は 1 です。一方、相対質量は 12C が 12 で、1H は 1.0078 です。
原子の質量は陽子と中性子の数でほとんど決まるので、各原子の相対質量は、それぞれの質量数に近い値になります。
原子量
各原子の質量は、相対質量として定まります。しかし同位体のある元素では、同じ元素でありながら、異なる質量数をもつ原子が複数あります。
このような同位体が存在する元素の原子の質量は、原子量で表します。
原子量とは、それぞれの同位体の相対質量に存在比をかけて、求めた平均値のことです。
ホウ素 B を例にして、同位体の相対質量と存在比から原子量を計算します。
ホウ素には質量数が 10 の ホウ素原子 10B が 19.9% の比率で、質量数 11 のホウ素原子 11B が 80.1% の比率で存在します。
また 10B の相対質量は 10.01 、11B の相対質量は 11.01 です。
それぞれの同位体の相対質量に存在比をかけて、総和である平均値を求めて原子量とします。
$$原子量 = 10.01 \times \frac{19.9}{100} + 11.01 \times \frac{80.1}{100} $$
これを計算すると 10.8 となり、ホウ素 B の原子量が 10.8 であるとわかりました。
なぜ原子量が必要か
ところで、なぜ原子量という値を考えなければいけないのでしょうか。各原子には相対質量があるので、それで十分のように思われます。
しかし、現実の世界にある物質を考えると、原子量が必要になってきます。
各同位体はそれぞれの質量数が違うだけで、化学的性質はほとんど同じなので、通常は同位体である原子を区別できません。
ある物質が同位体をもつ元素でできていた場合、その物質は同位体の存在比に従って複数の原子を含んでいます。
例えば、塩素ガス（塩素分子 Cl2 ）の入った瓶があったとします。この瓶の中にある塩素ガスの質量を考えるとき、原子量という値があった方が便利です。
塩素には同位体があり、質量数 35 の 35Cl は相対質量が 34.97 で存在比が 75.76% です。また質量数 37 の 37Cl は相対質量が 36.97 で存在比が 24.24% です。
塩素原子の原子量 35.45 は、以下のように求められます。
$$34.97 \times \frac{75.76}{100} ＋ 36.97 \times \frac{24.24}{100} ＝ 35.45$$
瓶の中には、相対質量 34.97 の塩素原子が 75.76% と、相対質量 36.97 の塩素原子が 24.24% 入っていると考え、それから全体の質量を計算するのは面倒です。
瓶の中に 相対質量 35.45 の塩素原子が 100% 入っていると考えて、それから質量を求める方が簡単です。
瓶の中の塩素原子（塩素ガス）は、相対質量 34.97 の塩素原子と相対質量 36.97 の塩素原子が、まったく区別することができない状態で混じり合っています。
ですから、質量が原子量 35.45 である塩素原子が瓶の中をすべて満たしている、と考えると簡便です。
分子量
分子の質量は、分子量で表します。分子の質量も 12C 原子を基準とするので、原子量の総和として計算できます。
分子量は、その分子を構成しているすべての原子の原子量を、すべて足し合わせた値です。
例として、水素 H2 や水 H2O 、塩素 Cl2 、塩化水素 HCl 、メタン CH4 の分子量を求めましょう。
それぞれの原子の原子量は H = 1.0 、C = 12.0 、O = 16.0 、Cl = 35.5 とします。
水素 H2 は水素原子が 2 個あるので、水素の分子量は
1.0 × 2 = 2.0 です。
水 H2O は水素原子が 2 個、酸素原子が 1 個あるので、水の分子量は
1.0 × 2 + 16.0 × 1 = 18.0 です。
塩素 Cl2 は塩素原子が 2 個あるので、塩素の分子量は
35.5 × 2 = 71.0 です。
塩化水素 HCl は水素原子が 1 個、塩素原子が 1 個あるので、塩化水素の分子量は
1.0 × 1 + 35.5 × 1 = 36.5 です。
メタン CH4 は炭素原子が 1 個、水素原子が 4 個あるので、メタンの分子量は
12.0 × 1 + 1.0 × 4 = 16.0 です。
式量
イオン結晶や金属結晶のように組成式で表される物質の質量は、式量で表します。
式量は分子量と同じように、組成式に含まれる原子の原子量の総和として求められます。
イオンの質量も、式量で表します。
イオンについても、含まれる原子の原子量の総和で計算できます。電子の質量は非常に小さいので、式量では無視します。
例として、塩化カリウム KCl や硫酸イオン SO42－ の式量を求めましょう。
それぞれの原子の原子量は O = 16.0 、S = 32.1 、Cl = 35.5 、K = 39.1 とします。
塩化カリウム KCl はカリウム原子が 1 個、塩素原子が 1 個あるので、塩化カリウムの式量は
39.1 × 1 + 35.5 × 1 = 74.6 です。
硫酸イオン SO42－ は硫黄原子が 1 個、酸素原子が 4 個あるので、硫酸イオンの式量は
32.1 × 1 + 16.0 × 4 = 96.1 です。
問題演習
確認テスト1
質量数 1 の水素原子 1H の相対質量を求めましょう。
炭素原子 12C 1 個の質量は 1.9926 × 10－23 g であり、水素原子 1H 1 個の質量は 0.16735 × 10－23 g です。
確認テスト2
塩素の原子量を求めましょう。
塩素には同位体があり、質量数 35 の 35Cl は相対質量が 34.97 で存在比が 75.76% です。また質量数 37 の 37Cl は相対質量が 36.97 で存在比が 24.24% です。
確認テスト3
二酸化炭素 CO2 と水 H2O の分子量を求めましょう。
それぞれの原子の原子量は H = 1.0 、C = 12.0 、O = 16.0 とします。
確認テスト4
塩化ナトリウム NaCl とアンモニウムイオン NH4+ の式量を求めましょう。
それぞれの原子の原子量は H = 1.0 、N = 14.0 、Na = 23.0 、Cl = 35.5 とします。
実践問題1（2020本第2問問1）
塩素 Cl には質量数が 35 と 37 の同位体が存在する。分子を構成する原子の質量数の総和を M とすると、二つの塩素原子から生成する塩素分子 Cl2 には、M が 70 、72 、および 74 のものが存在することになる。天然に存在するすべての Cl 原子のうち、質量数が 35 のものの存在比は 76 %、質量数が 37 のものの存在比は 24 %である。
これらの Cl 原子 2 個から生成する Cl2 分子のうちで、M が 70 の Cl2 分子の割合は何%か。最も適当な数値を、次の①～⑥のうちから一つ選べ。
① 5.8 ② 18 ③ 24 ④ 36 ⑤ 58 ⑥ 76
（2020年度センター試験 本試験 第2問問1 より引用）
正解 5
原子の質量数の総和 M が 70 となる塩素分子は、質量数 35 の塩素原子と質量数 35 の塩素原子が共有結合してできたものです。
同様に、原子の質量数の総和 M が 72 となる塩素分子は、質量数 35 の塩素原子と質量数 37 の塩素原子が共有結合してできたものです。
同様に、原子の質量数の総和 M が 74 となる塩素分子は、質量数 37 の塩素原子と質量数 37 の塩素原子が共有結合してできたものです。
質量数 35 の塩素原子は 76 ％の比率で存在しているので、質量数の総和 M が 70 の塩素分子となる割合は 76% × 76% ≒ 58% です。
実践問題2（2017追第1問問5）
カリウムは、原子量が 39.10 であり、39K（相対質量 38.96 ）と 41K（相対質量 40.96 ）の二つの同位体が自然界で大部分を占めている。これら以外の同位体は無視できるものとし、41K の存在比として最も適当な数値を、次の①～⑧のうちから一つ選べ。
① 1.0% ② 5.0% ③ 7.0% ④ 49%
⑤ 51% ⑥ 93% ⑦ 95% ⑧ 99%
（2017年度センター試験 追試験 化学基礎 第1問問5 より引用）